Règle des scribes: diviser un nombre n par un nombre m (régulier en base 60), c'est multiplier n par l'inverse de m. Exemples. Pour diviser 50 par 30, on multiplie 50 par 2 car l'inverse de 30 est 2. Pour diviser 1.40 par 7.30, on multiplie 1.40 par 8 car l'inverse de 7.30 est 8.. L'activité de la semaine : Illustrer la division de deux fractions. Pour diviser une fraction par une autre fraction, il faut la multiplier par l'inverse de cette dernière. En tant qu'enseignant, cet énoncé est tout à fait logique. Toutefois, le concept peut être déroutant pour de nombreux élèves. La maîtrise de l'algorithme.

Multiplier Diviser par 0,1 0,01 et YouTube

PPT CHAPITRE 5 Fractions PowerPoint Presentation, free download ID3112543

Multiples et diviseurs YouTube

quatrième inverse et division de fractions YouTube

numérateur et dénominateur d'une fraction

Multiplier ou diviser deux expressions rationnelles monomes YouTube

Multiplier et diviser les fractions 4ème Leçon et exercices

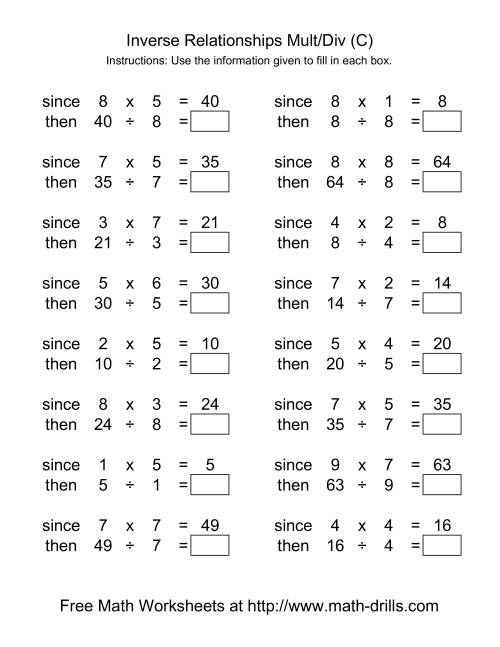
Inverse Relationships Multiplication and Division Range 1 to 9 (C)

Cours de Maths / 4e 2016 CH 9 Inverse

Multiplier et diviser poser les opérations YouTube

POURQUOI DIVISER c'est MULTIPLIER par l'INVERSE ? YouTube

COMMENT CALCULER UN INVERSE ET DIVISER DEUX FRACTIONS ? YouTube

apprendre a faire les divisions cm1

Fiche complète sur les multiples et les diviseurs KeepSchool

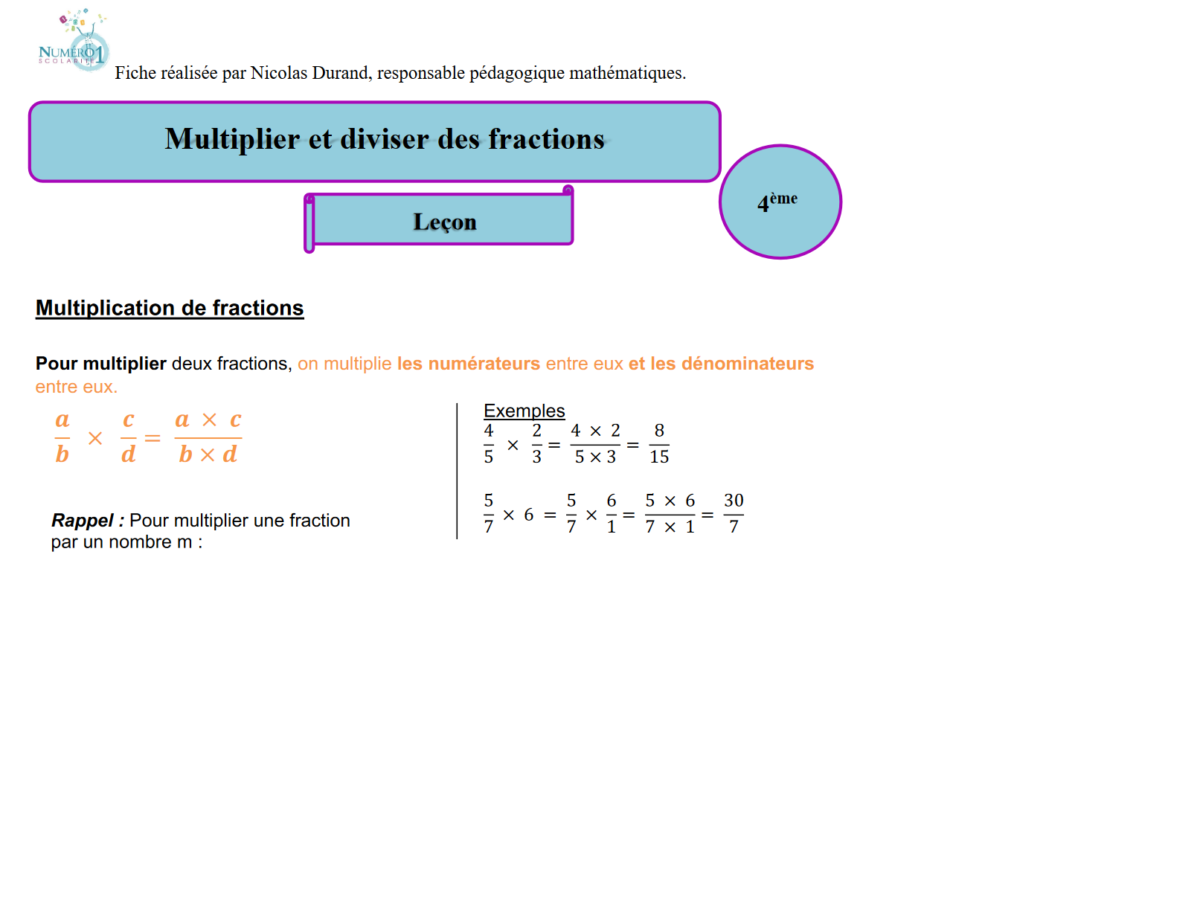
Multiplier et diviser les fractions 4ème Leçon et exercices

Mathématiques cours sur les multiplications en maths en 6è

multiplication et division de fraction 4eme exercices

Diviser Revient A Multiplier Par Son Inverse Exemple Divers Exemples

Multiplicative inverse, Math Lecture Sabaq.pk YouTube

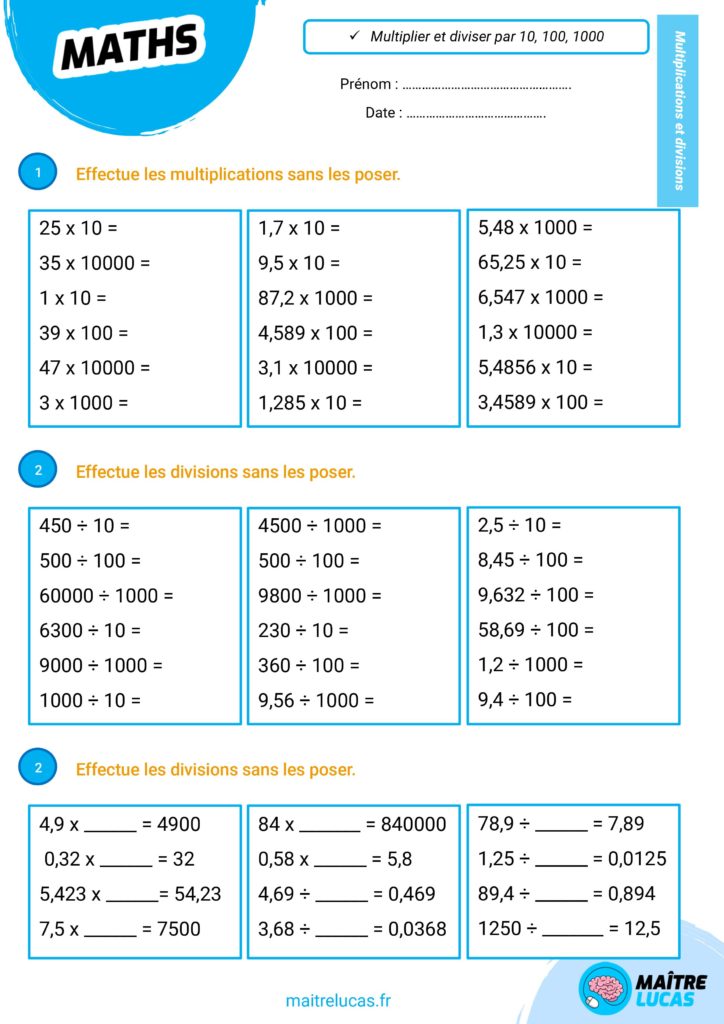
Exercices Multiplier et diviser par 10, 100, 1000... CM1 CM2 Maître Lucas

Retrouvons maintenant le zéro : diviser par celui-ci reviendrait donc à multiplier par l'inverse de zéro. Et c'est ici que la machine se grippe. Prenons z, un nombre quelconque.. L'inverse de - 3 7 est - 7 3 car - 3 7 × - 7 3 =1 II. Divisions de fractions Règle : Diviser par un nombre non nul revient à multiplier par son inverse. Ainsi, on a : - Si a et b désignent deux nombres relatifs avec b≠0 alors : a÷b= a b =a× 1 b. En effet, on veut diviser a par b et finalement on voit que cela revient à.