スポンサーリンク 円周 \(=\) 直径 \(\times\) 円周率 練習問題① 直径が 4cm の円周を求めてみましょう。ただし円周率は 3.14 とします。 円周を求める公式は \[ 円周 = 直径 \times […]. このページでは、例題と共に、円周の求め方を説明しています。 お使いのブラウザでは JavaScript が無効になっています。 当サイトは数式表示に JavaScript を利用しているため、これを無効にしているとページが正しく表示されません。

円周角と円の外の点を結んで /おときち副塾長 電脳空間学習塾かもん YouTube

円周角の定理とは?性質や証明、定理の逆、中心角との関係や求め方などを徹底解説! 受験辞典

円周の求め方!公式は直径を使うので、半径と間違えないように! 中学や高校の数学の計算問題

円周角の定理とは?性質や証明、定理の逆、中心角との関係や求め方などを徹底解説! 受験辞典
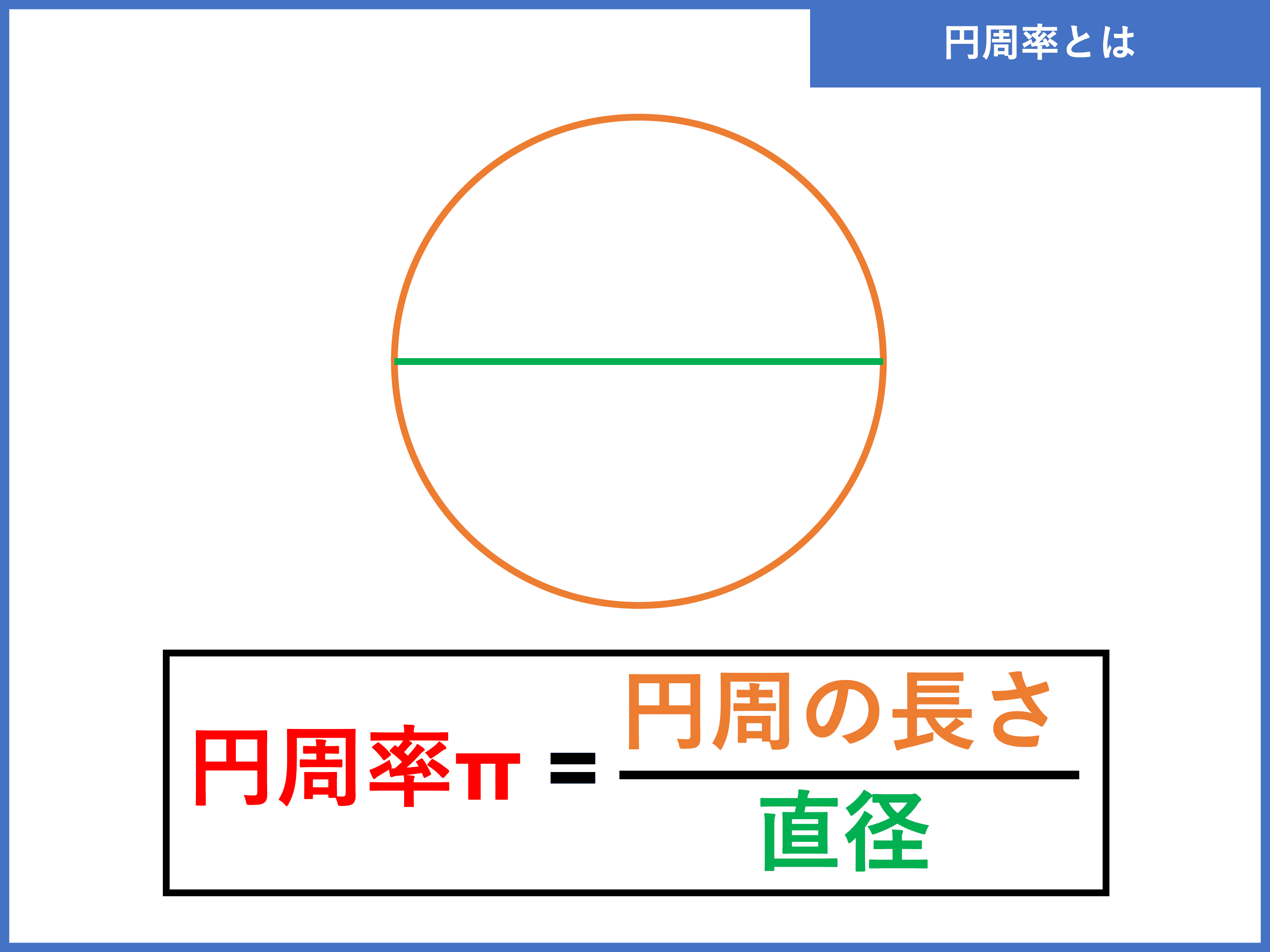
円周率πとは?求め方や、100桁までの覚え方をご紹介! 受験辞典
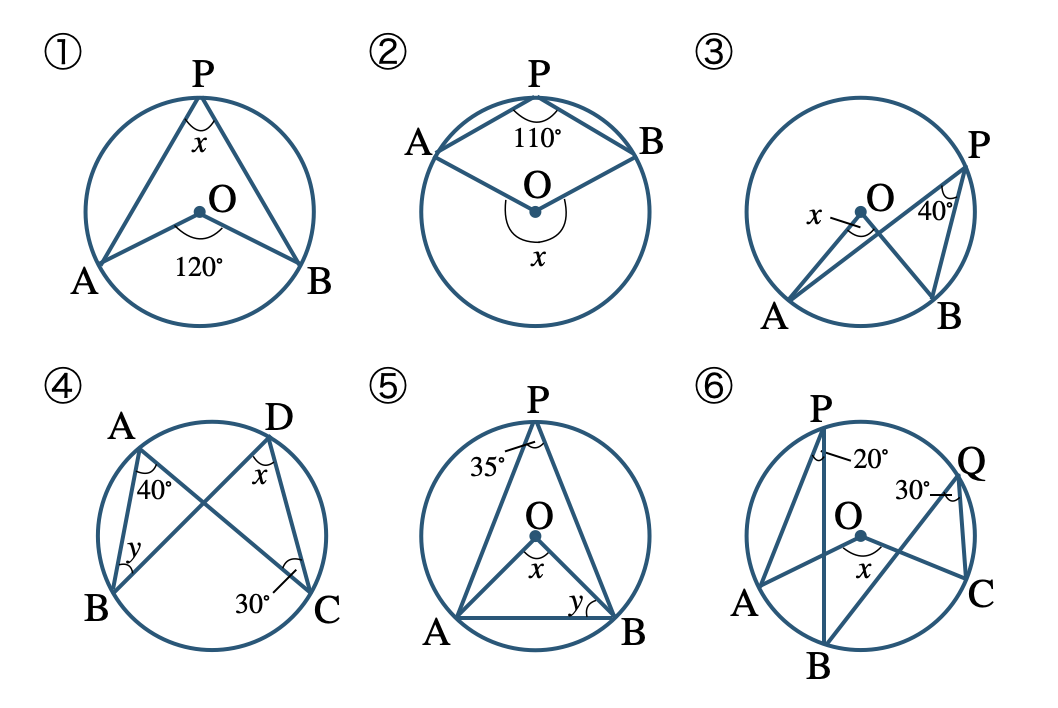
中3数学|円周角の定理の解き方とコツ 教科書より詳しい中学数学

円周角の定理とは?性質や証明、定理の逆、中心角との関係や求め方などを徹底解説! 受験辞典
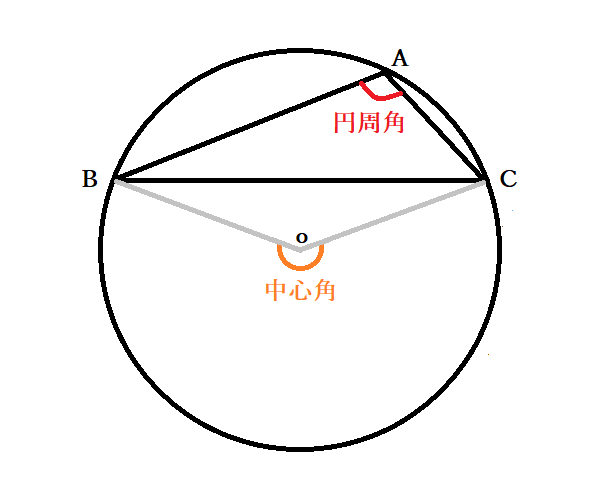
【中3数学】円周角の定理とは?円周角と中心角の関係の証明法、円の性質の応用問題/中学 Curlpingの学びblog
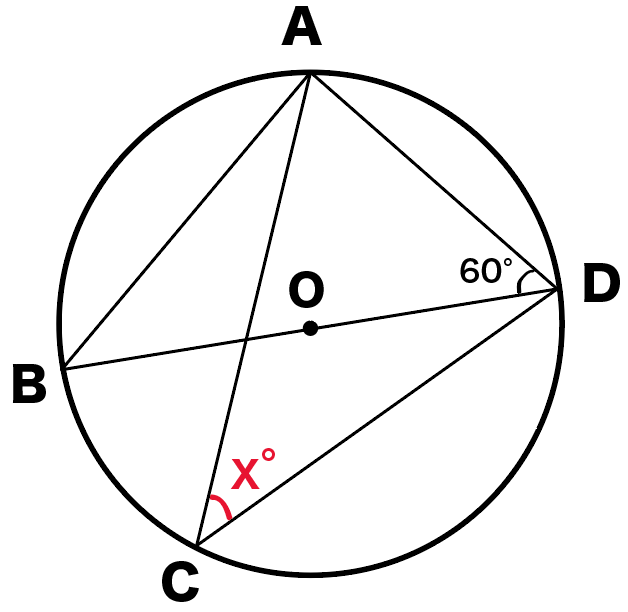
円周角の定理で角度を求める問題の解き方3ステップ Qikeru:学びを楽しくわかりやすく
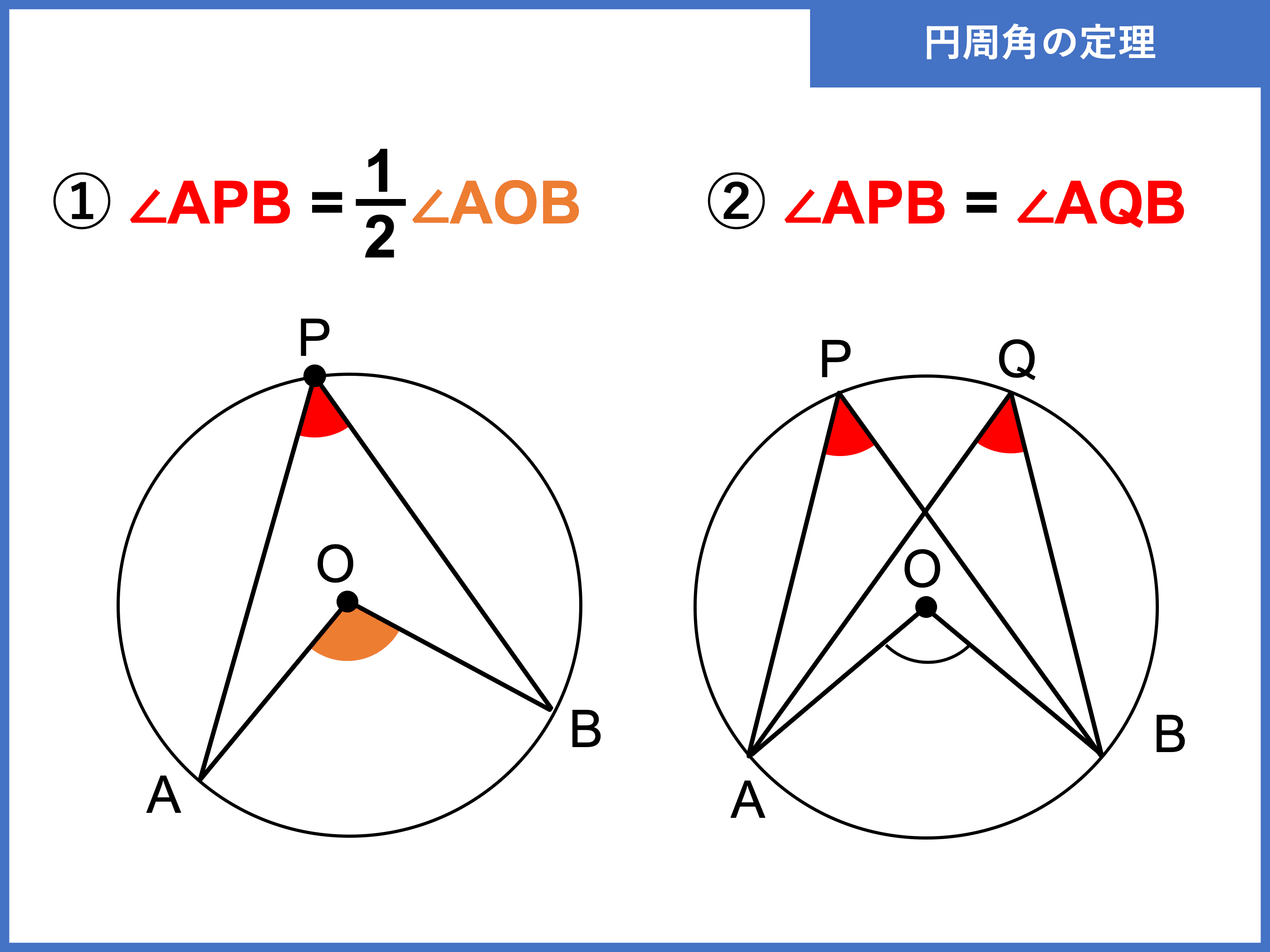
円周角の定理とは?性質や証明、定理の逆、中心角との関係や求め方などを徹底解説! 受験辞典
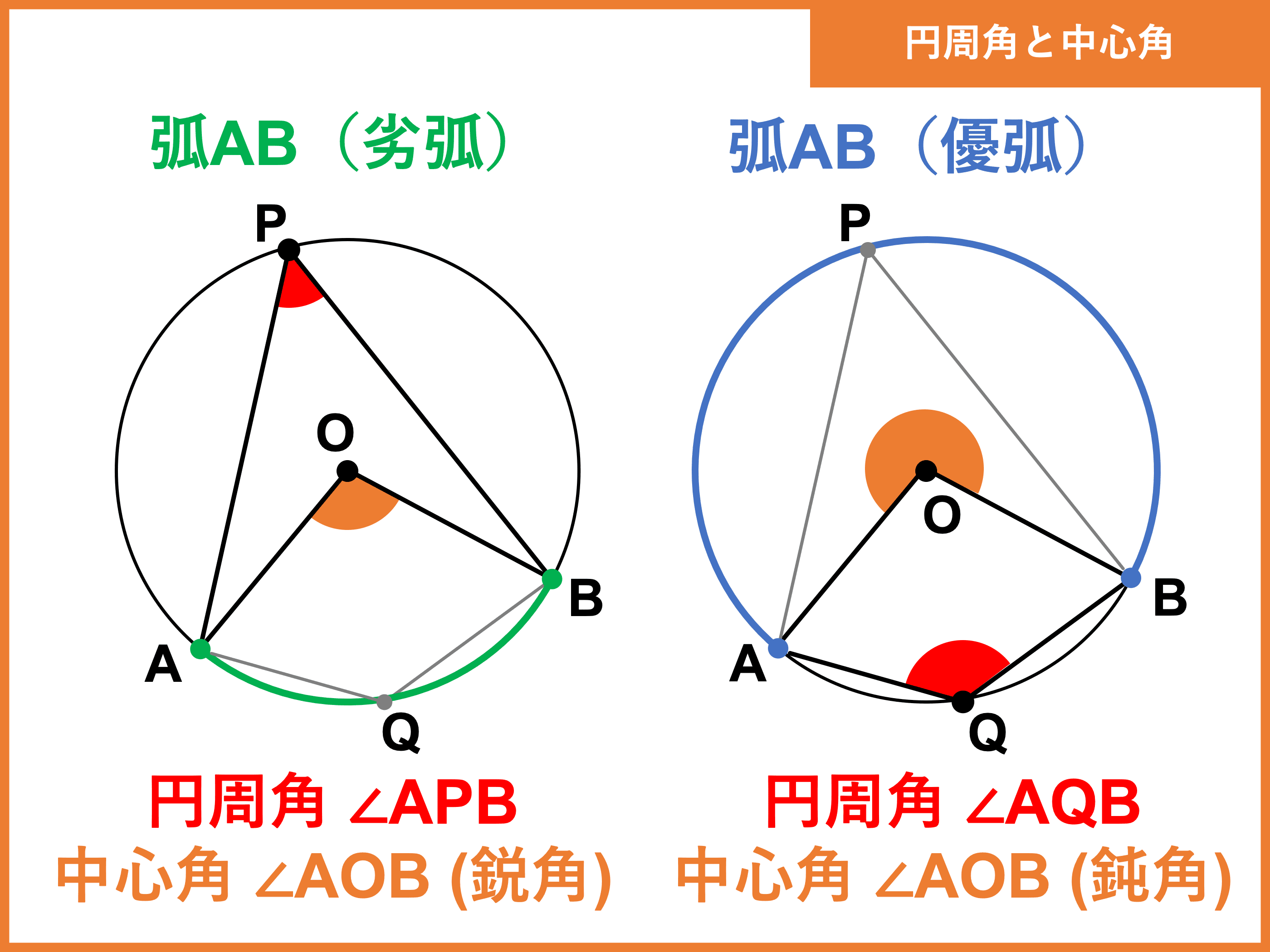
円周角の定理とは?定理の逆や証明をわかりやすく解説! 受験辞典
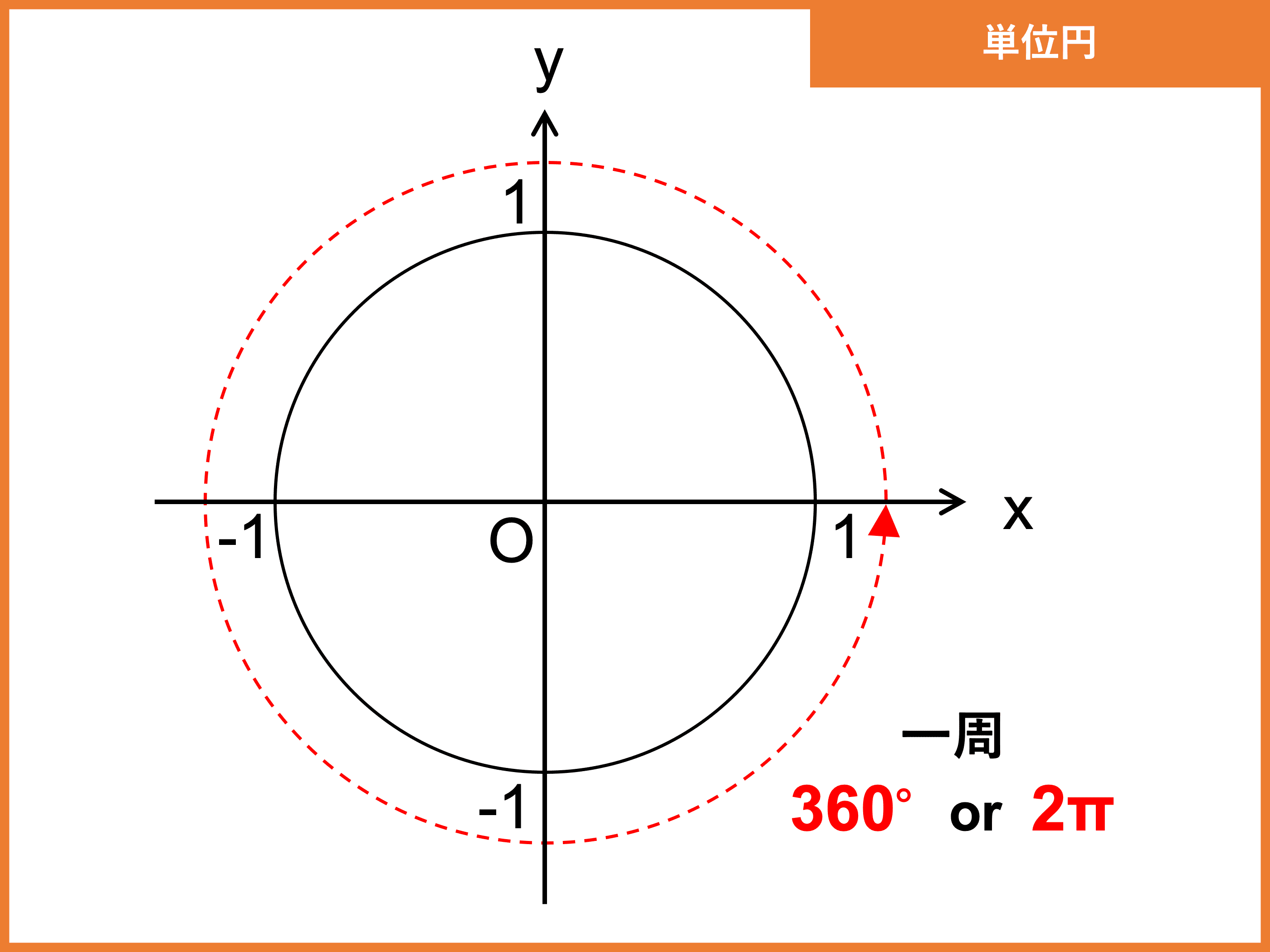
三角関数の角度の求め方と変換公式をわかりやすく解説! 受験辞典
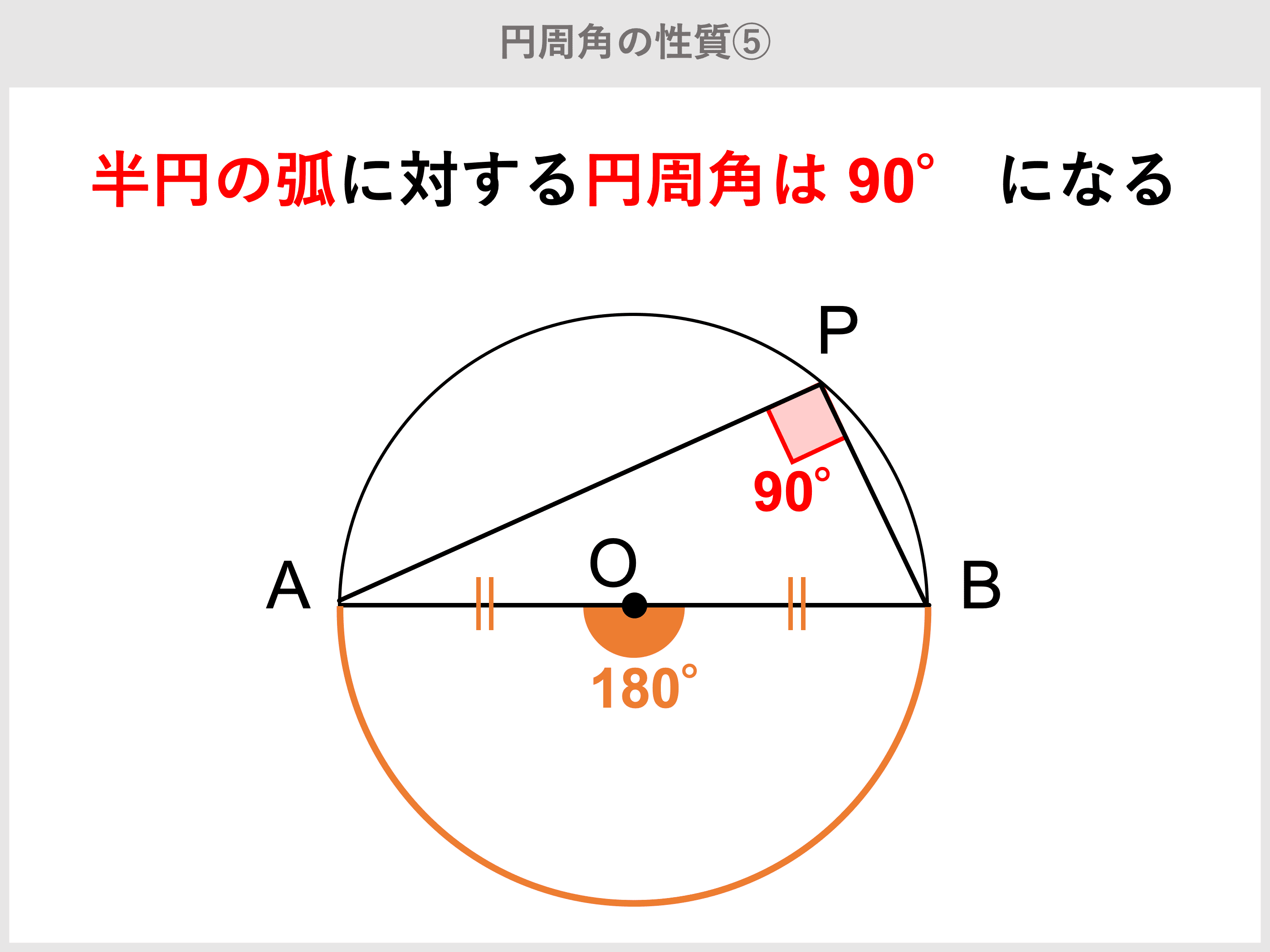
円周角の定理とは?定理の逆や証明をわかりやすく解説! 受験辞典

5年生~6年生 円の面積・円周の求め方と問題たっぷり ガルボズラボ
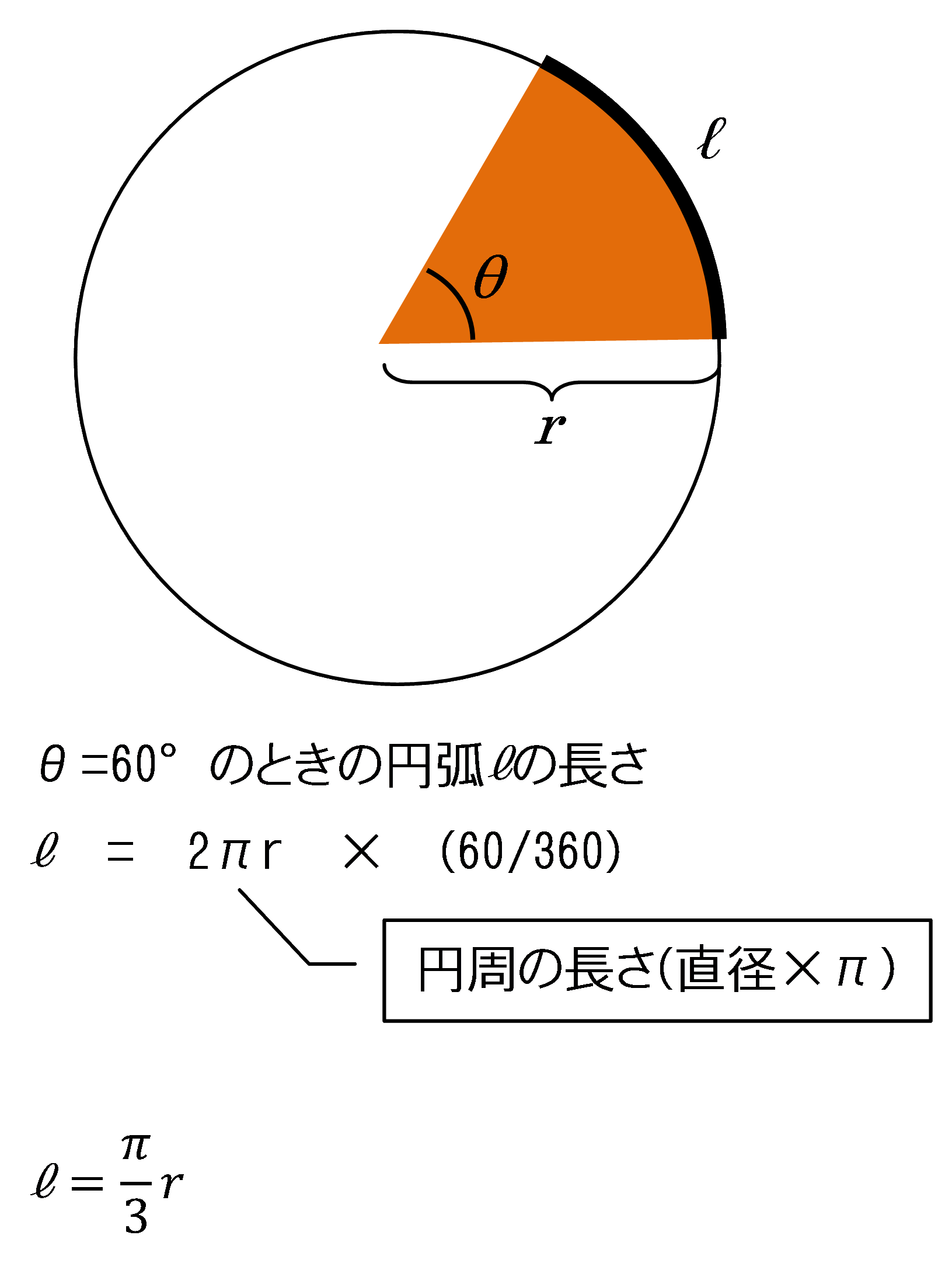
円運動:物理学解体新書

媒介変数表示とは?グラフや計算(微分積分・ベクトル) 受験辞典

円周角の定理と証明、中心角の求め方を詳しく解説! Rike English
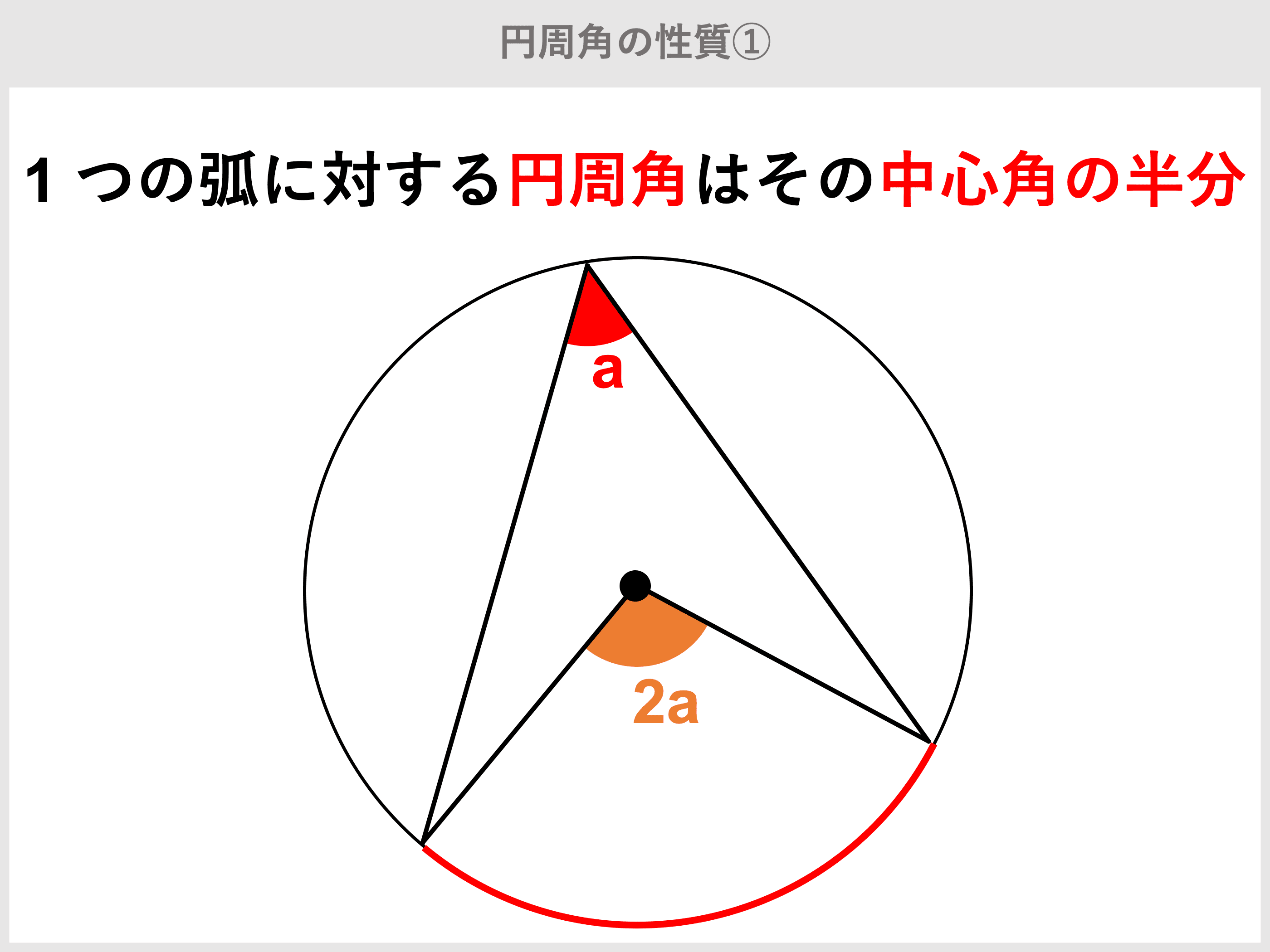
円周角の定理とは?性質や証明、定理の逆、中心角との関係や求め方などを徹底解説! 受験辞典
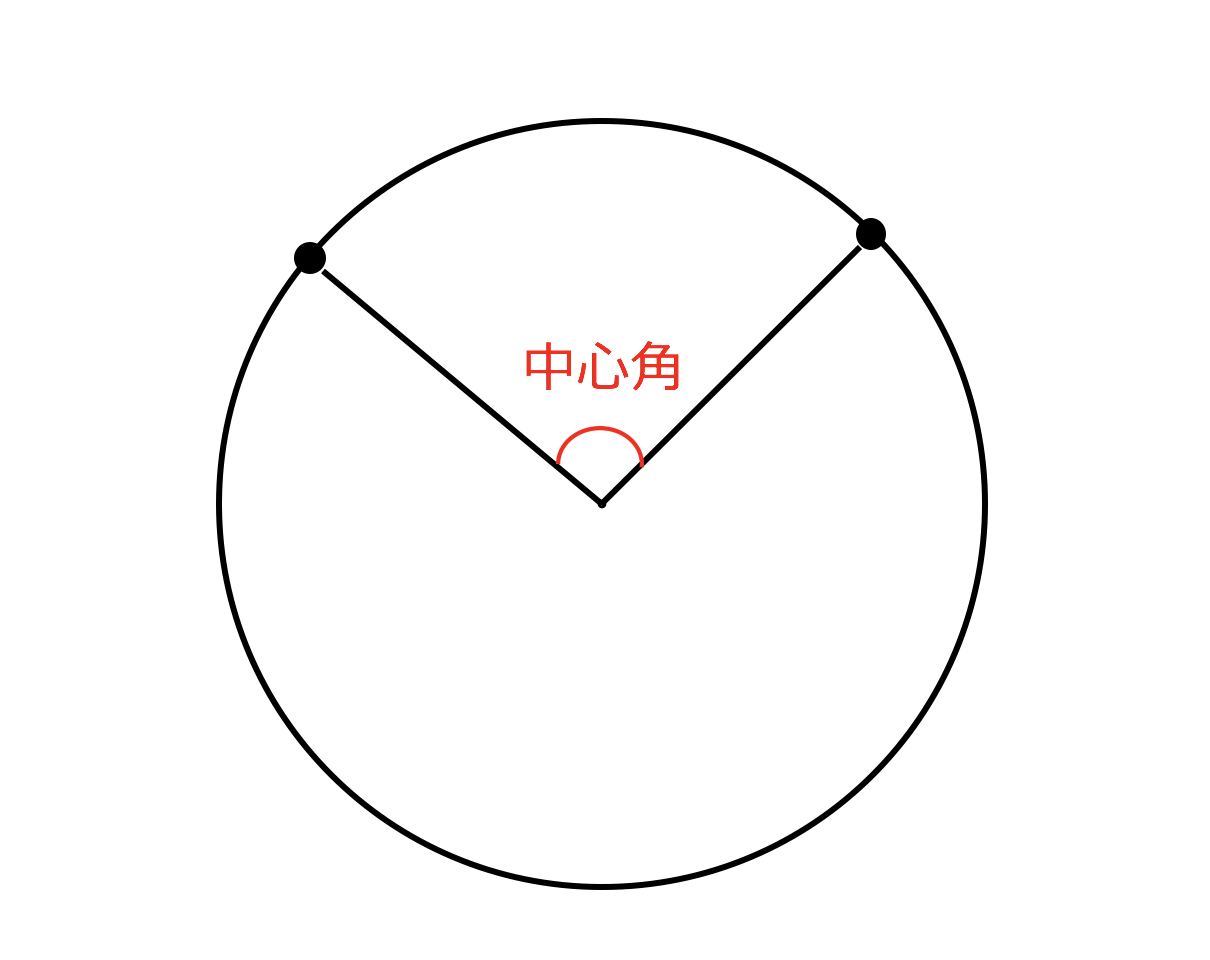
円の中心角の求め方 134862円の中心角の求め方
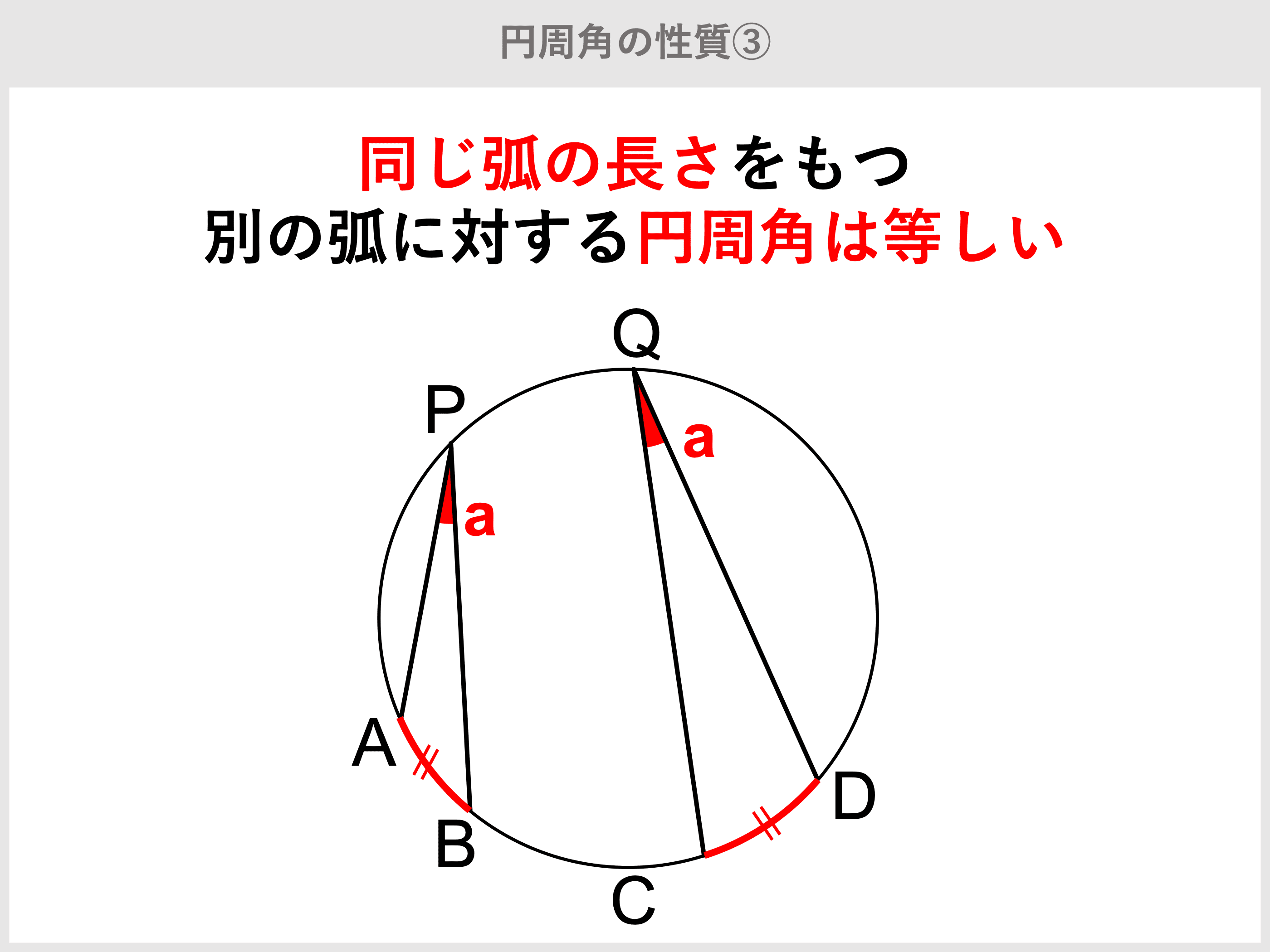
円周角の定理とは?性質や証明、定理の逆、中心角との関係や求め方などを徹底解説! 受験辞典
中学3年の数学で学習する「円周角の定理」。定理自体は理解できていても、実際に問題として出されると、どのように使えばよいのかわからなくなってしまう人も多いのではないでしょうか。そこで今回は、円周角の定理をわかりやすく解説するとともに、つまずきやすい証明問題の解き方を.. 円周を 等分する点の問題の解き方. 等分する弧1つの中心角を求める(360°÷ ). 求める角に関する円周角を作る. (慣れてくれば、等分する. 弧1つの円周角→180°÷ を使っても良いです). 円周角と中心角のまとめ. ①円Oで$\stackrel{\huge\frown}{AB}$を除いた. 円.