片持ち梁の固有振動数 その1. 振動. 梁の 運動方程式 が出たので，ついでといっては何ですが 固有振動数 のお話です. 片持ち梁の一次モードの振動を考えます. 梁の長さを l，単純曲げ変形のみとし，E，A，I，γは一定とします. frequency_cantilever.wxm. y : 梁のたわみ関数. Xt : 時間発展を表す関数. y が位置 x と時間 t の関数であること，Xt が t の関数であることをそれぞれ%o1, %o2式で宣言します（画面出力は省略） 連続体の梁の 運動方程式 を%o3式に示します. 梁の 運動方程式 の導出については 運動方程式とラグランジアン その4 を参照ください. Xm : モードを表す関数.. 片持ち梁の振動を利用した実験を行いたいのですが，固有振動数の計算方法に関して不明な点があります．まず，単純な片持ち梁の固有振動数については下記の式で算出できると思います．f=(λ/2πL)√(Eg/γ) [Hz]ただし，・λ：境界条件

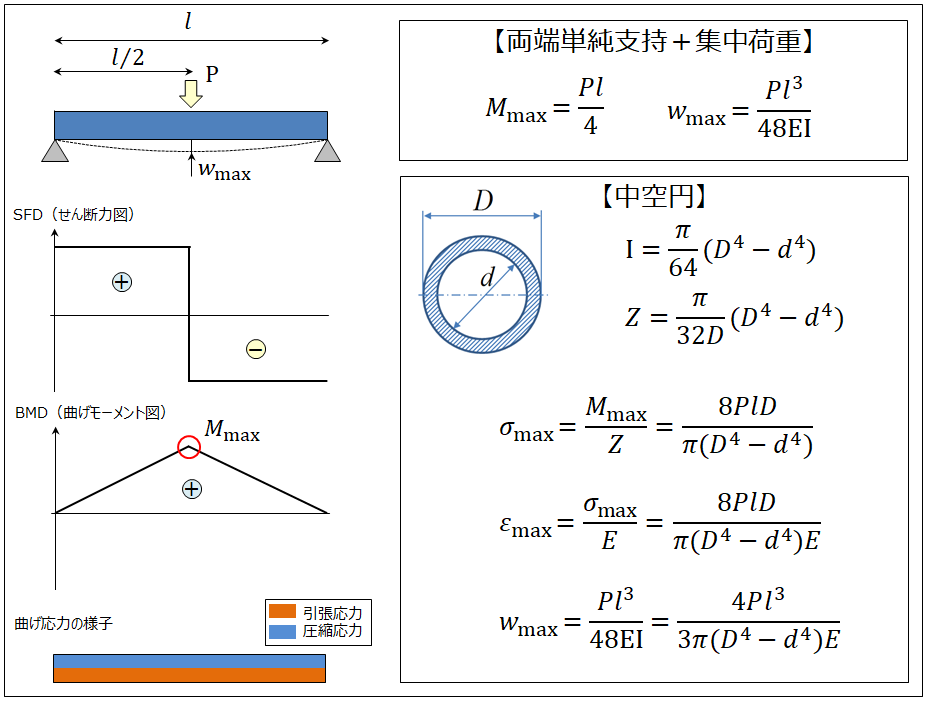
はりの強度計算 【両端単純支持－集中荷重－中空円（管／パイプ）】

はりの強度計算 【片持ちはり－集中荷重－台形】 製品設計知識

片 持ち 梁 曲げ モーメント 図

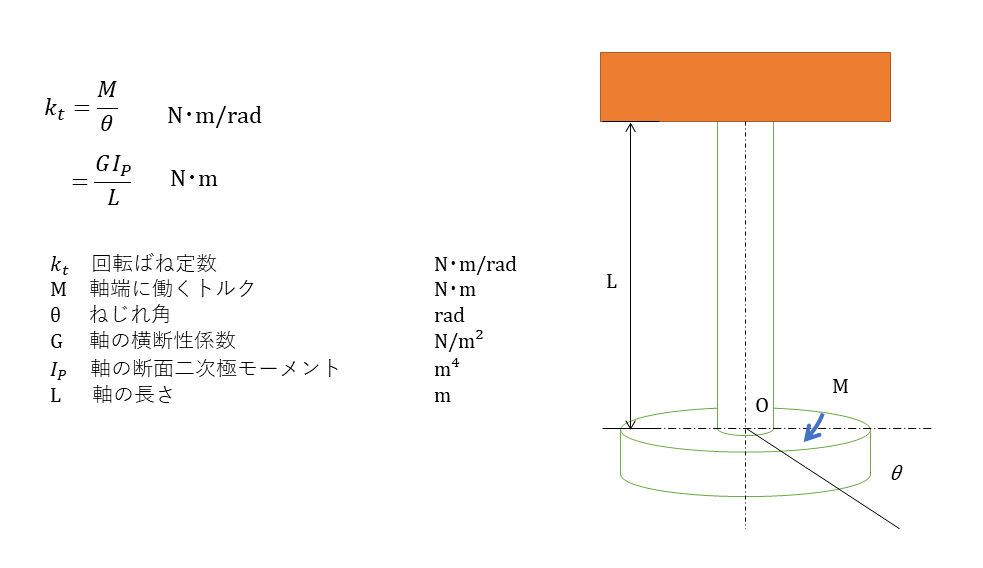
ねじり振り子 Hitopedia

梁のたわみの基礎方程式から，振動数方程式を導出する

片 持ち 梁 たわみ 集中 荷重 途中

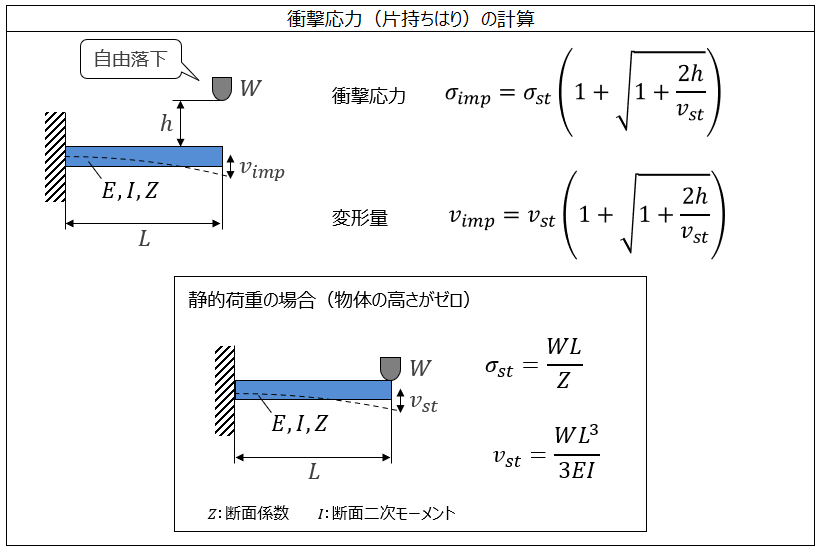
衝撃応力（片持ちはり）の計算 製品設計知識

Arduinoでロボットを作ってみました！【10】動作試験Part1：首関節が痙攣してる!! MS Design

自由大学

【固有値解析】コスパ最強！固有振動数解析と共振回避の方法 CAE受託ドットコム

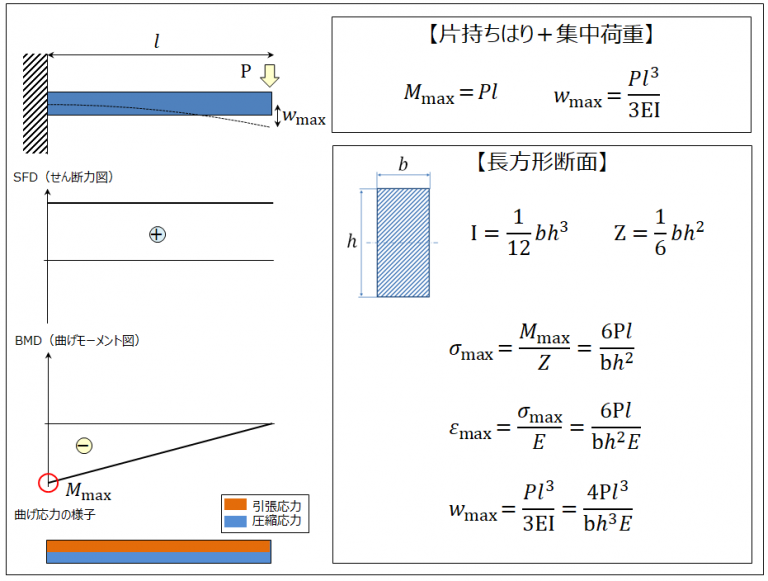
はりの強度計算（3）～プラスチック製品の強度設計～ 製品設計知識

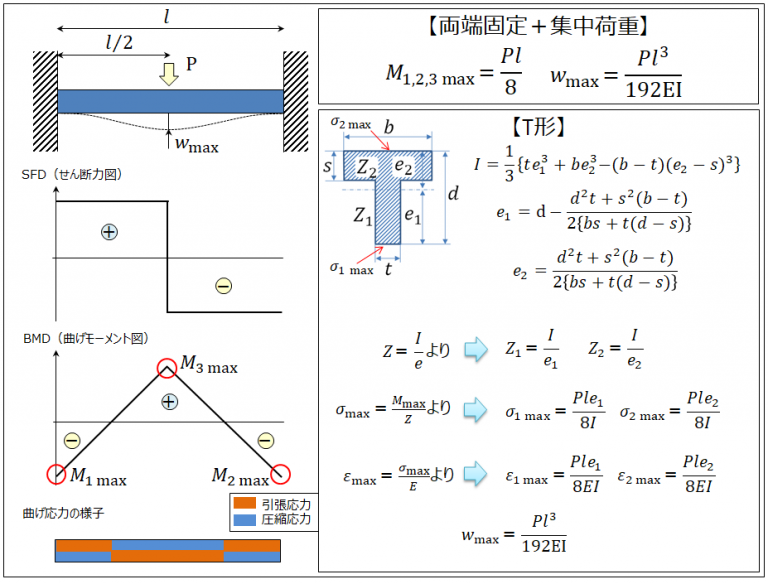
はりの強度計算 【両端固定ー集中荷重ーT形】 製品設計知識

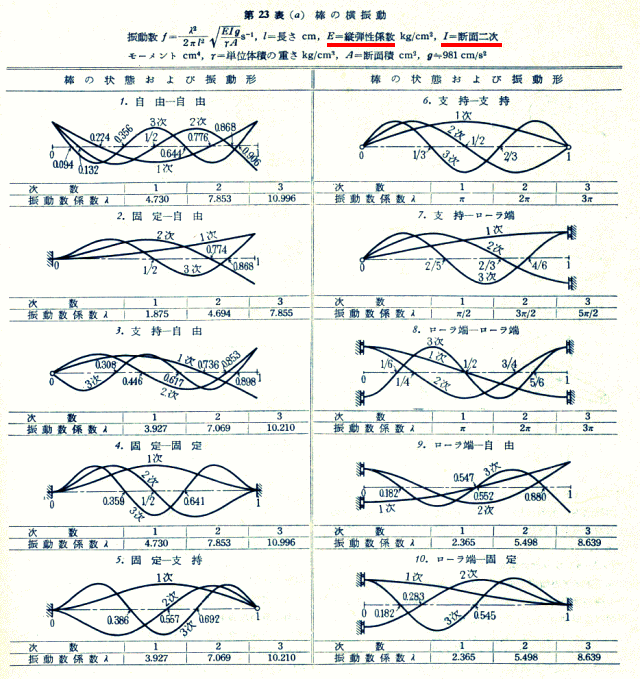
弓の力学 スティックの固有振動数

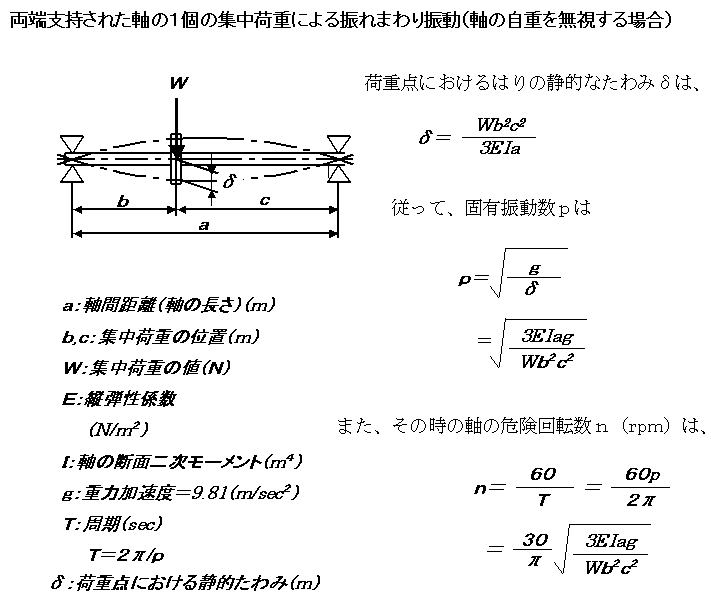
工業力学入門講座（第29回） 固有振動数

片 持ち 梁 たわみ 集中 荷重 途中

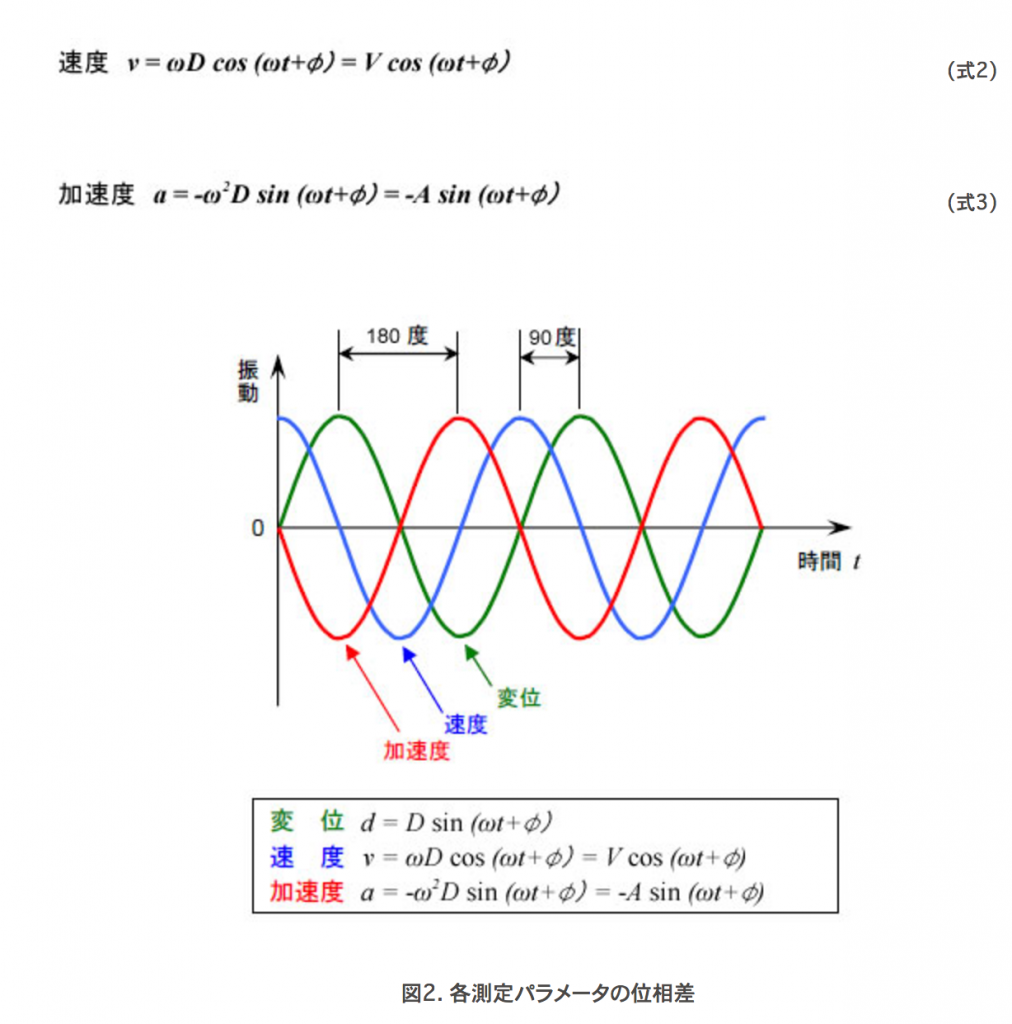
【振動の三種類の測定パラメータ】vol.1 調和振動における変位、速度、加速度の関係 ものづくりニュース by アペルザ

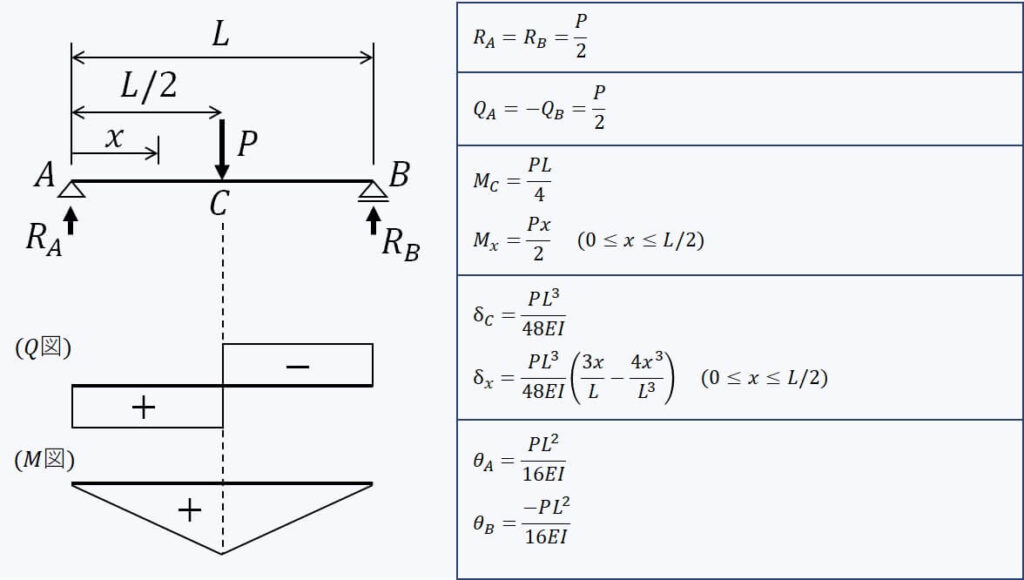
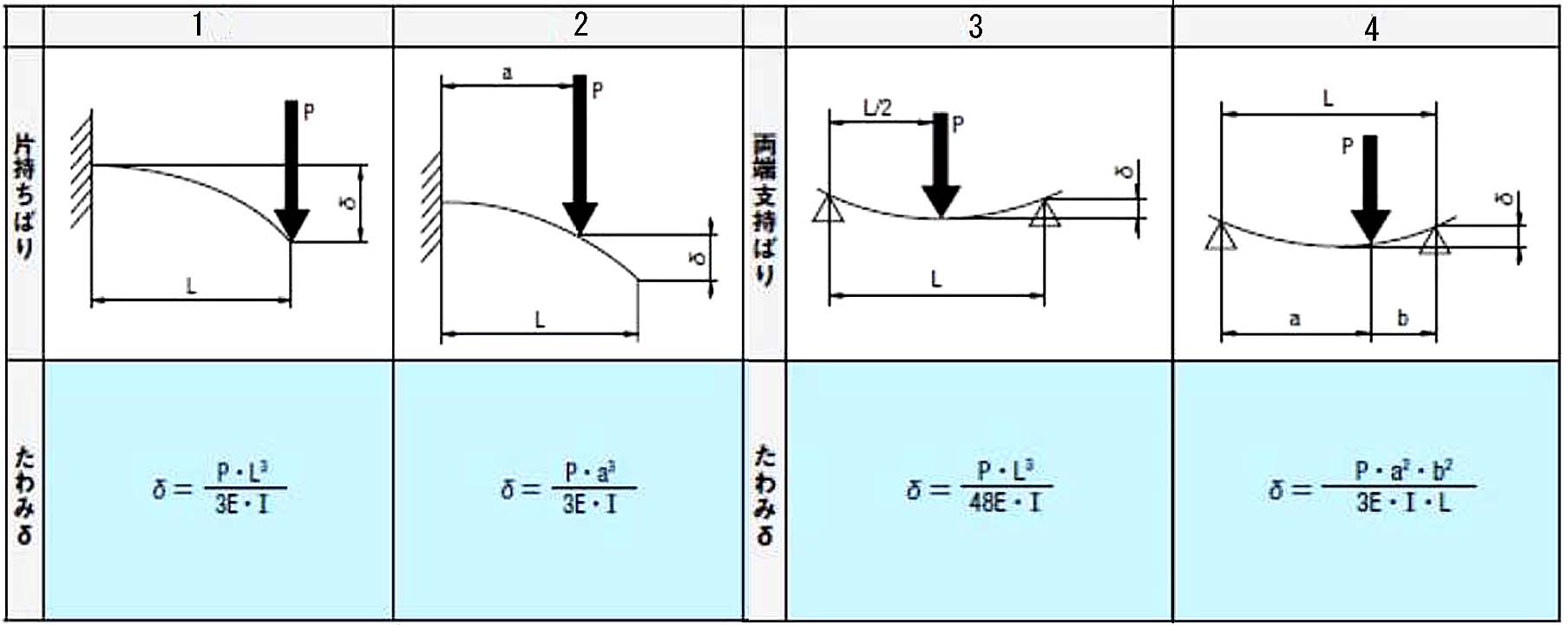
梁の曲げモーメント公式・たわみ公式一覧【構造計算公式集】 1分で分かる土木工学

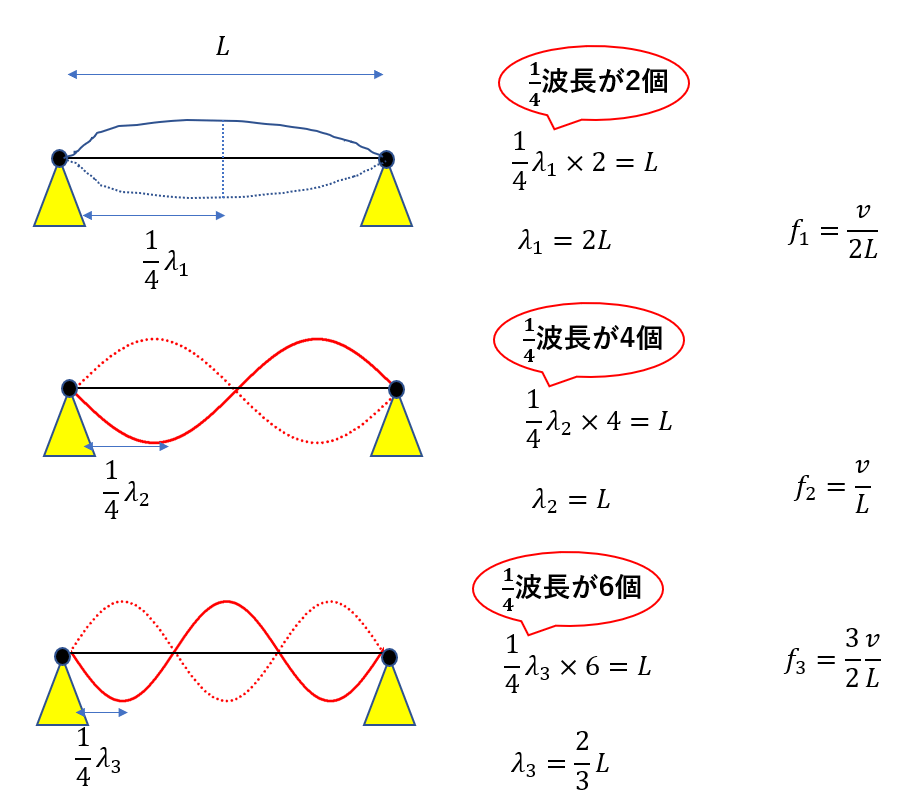
【物理基礎】弦の振動の公式とは？導出も問題もイメージで突破せよ！ 受験物理 Set Up

【頭に残る！】わかりやすい構造力学各種梁のたわみ量まとめ 梁, 記録術, 物理学

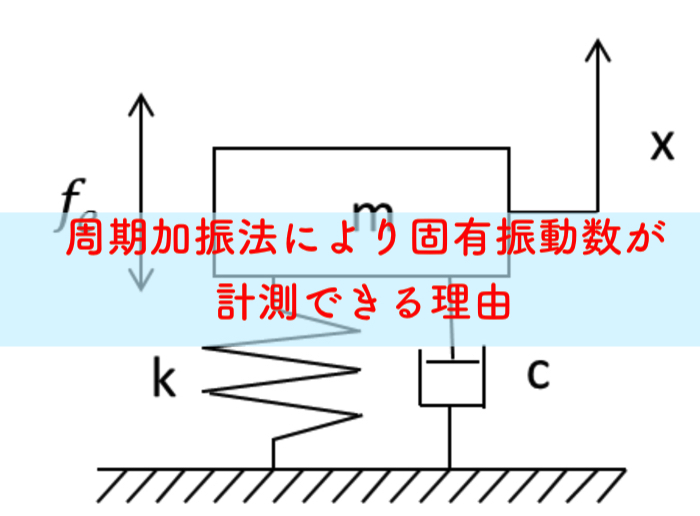
梁や板に加振（周期，打撃）したときの固有振動数と固有モードを計測する実験

連続体の振動は,質量とばねが全体に分布したものであり,多自由度系の自由度が無限に大きくなったものと考えることができる。 従って,固有振動数は無限個のとびとびの値となり,固有ベクトルは各部分の振幅を表す場所xの関数となる。 弦の振動,棒の縦振動,コイルばねの縦振動,気柱の振動,棒のねじり振動等は,連続体の振動として扱うことになる。 それぞれの対象について,下記のu(x; t)を未知の変数とする。 これは多数の重りとばねが連結された多自由度系の各重りの座標u1(t); u2(t); u3(t); ¢ ¢ ¢ ; un(t)に対応する。 8. >>つり合い位置からの弦の横方向変位<つり合い位置でx の位置にある部材面の縦方向変位u(x; t). 片持ち梁の表す式として、一般的なf= (1.875/L)^2/2π√EI/ρA (1次モード）と、先端負荷荷重mのある場合のf= (1/2π)√ {EI/ (ρAl/3+m)l^3}があります。 後者の先端負荷荷重m=0とした場合は前者の式と一致するはずでは？ と思ったのですが、実際には一致しません。 どなたかその理由を教えてください。 よろしくお願いします。 通報する. この質問への回答は締め切られました。 質問の本文を隠す. 回答(2件) 最新から表示. 回答順に表示. No.2. 回答者： inara. 回答日時： 2007/01/21 21:12. ANo.1です。